「標準偏差はいつも同じものを使っている」「n−1で割る理由は正直よくわからない」――そんな状態でも、日々の業務はなんとなく回ってしまいます。
しかし、目的と指標がズレたまま統計量を使うことは、判断ミスや誤解の原因になります。
本記事では、現場でありがちな勘違いを整理しながら、不変分散・不変標準偏差と標本分散・標本標準偏差の違いを、実務で使える形で解説します。
なぜ分散・標準偏差が重要なのか
分析結果や測定データを評価するとき、平均値だけを見て判断してしまうことは少なくありません。 しかし、平均が同じでも、データのばらつきが大きく異なるケースは多く存在します。
- 測定値が安定しているのか
- たまたま良い(悪い)値が出ただけなのか
- 判断に使えるデータなのか
こうした点を見極めるために使われるのが、分散や標準偏差です。
勘違いされやすいポイント
不変標準偏差は「上位互換」ではない
不変標準偏差という名前から、「標本標準偏差より正確」「とりあえず使えば安心」と思われがちです。 しかし、これは誤解です。
両者の違いは精度の優劣ではなく、目的の違いにあります。
- 標本標準偏差:手元のデータのばらつきを表す
- 不変標準偏差:母集団のばらつきを推定する
役割が異なるだけで、どちらが優れているという話ではありません。
n−1は暗記するものではない
不変分散・不変標準偏差では、分母が n ではなく n−1 になります。 これを「そういう決まりだから」と暗記してしまうと、使い分けができません。
ポイントは、標本平均を使った時点で自由度を1つ失っているという考え方です。 そのまま n で割ると、ばらつきを小さく見積もってしまうため、n−1で補正します。
標本分散・標本標準偏差とは
何を表している指標か
標本分散・標本標準偏差は、手元にあるデータそのもののばらつきを表す指標です。 いわゆる「記述統計」に分類されます。
- 実際に測定した値がどれくらい散らばっているか
- データの安定性はどうか
こうした点を把握するために使います。
実務での使いどころ
- 日常の測定結果チェック
- 複数データのばらつき比較
- 報告書やグラフへの記載
「このデータはどれくらいバラついているか」を知りたいだけなら、標本標準偏差で十分です。
不変分散・不変標準偏差とは
「不変」の本当の意味
不変分散・不変標準偏差は、母集団の分散・標準偏差を推定するための指標です。
標本から計算した分散は、平均を使う影響で本来より小さくなりがちです。 その偏りを補正したものが「不変(偏りがない)」分散・標準偏差です。
実務での使いどころ
- 信頼区間の計算
- 仮説検定
- 工程能力指数(Cp、Cpk)
「この結果から全体を判断したい」「推定や判定に使いたい」場合に使われます。
両者の違い
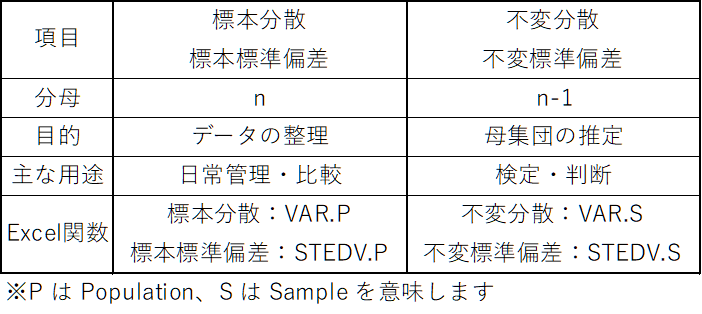
ケース別・正しい使い分け
- データの傾向や安定性を確認したい → 標本標準偏差
- 結果から全体を推定・判断したい → 不変標準偏差
迷ったときは、「記述か、推定か」で考えると判断しやすくなります。
まとめ
- 不変分散・不変標準偏差は万能ではない
- 標本分散・標本標準偏差は実務で十分役立つ
- 大切なのは「どちらが正しいか」ではなく「目的に合っているか」
統計量は、正しく使ってこそ意味を持ちます。 目的に応じて使い分けることで、データは判断の武器になります。



コメント