平均値は便利な指標ですが、外れ値が混ざった瞬間に “判断を狂わせる数字” に変わります。
品質管理、分析結果の評価、業務データの集計など、どの現場でも平均値だけで判断したことによるトラブルは少なくありません。
そこで活躍するのが 中央値(Median) です。
本記事では、現場で本当に使える「平均値と中央値の使い分け」を、実例を交えて解説していきます。
平均だけで判断すると現場で起こるズレ
データ分析や品質管理では「とりあえず平均」で判断しがちです。
しかし平均は外れ値に弱く、少数の異常値に全体が引っ張られます。
- トレンドが改善しているように見える
- 平均残業は減ったのに現場の負担は変わらない
- 分析値の外れ値で品質評価が狂う
平均という指標は便利ですが、使いどころを間違えると誤判断につながります。
平均値と中央値の違い
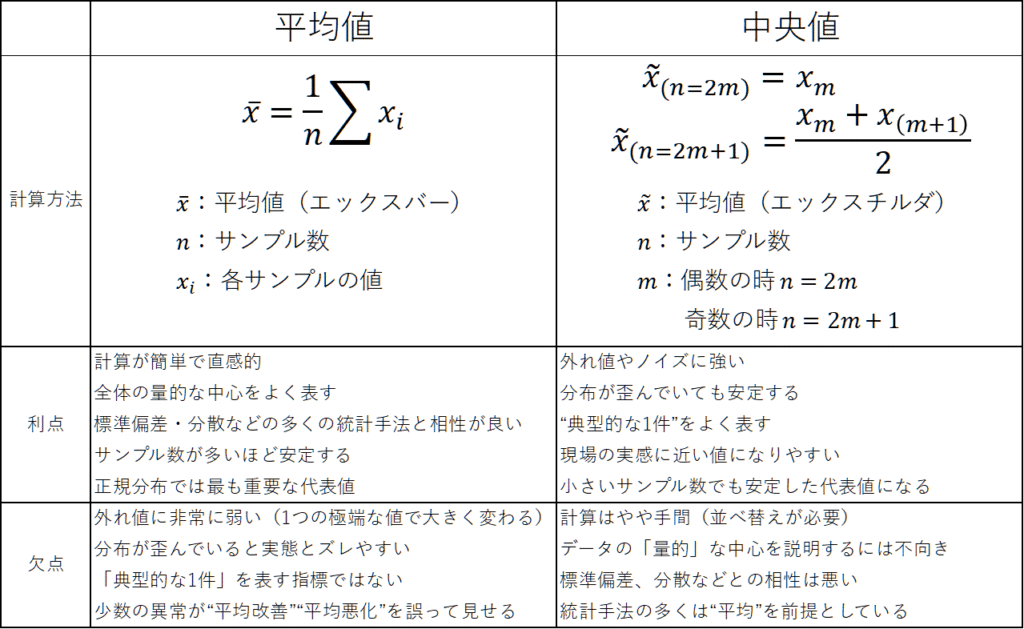
平均値を使うべきケース
データが正規分布に近い場合
機器の校正値や温度・湿度の自然変動など、誤差がランダムに発生する現象は正規分布に従うため、平均値を用います。
- 分散や標準偏差が意味を持ちやすい
- 管理図との相性が良い
- 統計的検定の多くは平均を前提にしている
データ数が十分多い場合
母数が大きければ外れ値の影響は相対的に小さくなります。
大量のデータから「全体の傾向」をつかみたいときは平均が効果的です。
“量的な中心”を知りたいとき
工程能力指数(Cp、Cpk)やσの評価など、変動そのものを把握する分析では平均は欠かせません。
中央値を使うべきケース
外れ値・ノイズが混ざりやすいデータ
分析値にありがちな“ときどき跳ねる値”。濁度、騒音、pH、濃度など、機器のドリフトや環境変動の影響で外れ値が出ます。
そのようなデータの代表値に平均を使うと、1件の異常値に全体が大きく影響されます。
中央値なら、外れ値に左右されにくく、「典型的な値」を安定して把握できます。
分布が歪んでいるケース
年収データ、サイクルタイム、顧客単価など、現場データの多くは「低いほうに寄っていて、右側に長く伸びる」分布です。
このような場合、平均値は“高め”に引っ張られ、実態とズレます。中央値のほうが“現場の感覚に一致する数値”になることが多いです。
“典型的な1件”を知りたいとき
工程の実態、顧客の典型的行動、作業時間の中心値など、「どんな状態が標準なのか?」を知る目的の場合、中央値が適しています。
平均値だけを使ったときによくあるトラブル
QCトレンドの誤判断
月ごとの分析値を平均すると、数件の低値・高値に引っ張られて“改善しているように見える”ことがあります。
中央値を見ると緩やかに悪化しているケースも多く、トレンド把握を誤る原因になります。
工程異常の見落とし
工程時間・待ち時間などのデータは歪んだ分布になりがちです。
平均だけで見ると異常を察知できず、中央値や四分位範囲で見たら“明確な詰まり”が見えることもあります。
分析値レポートの実態ズレ
JIS法では平均採用が多いですが、現場判断においては中央値の方が意味を持つ場面があります。
特に“外れ値が出やすい測定”では、中央値の方が安定します。
データを用いた比較
例1:外れ値が混ざった分析値10点
10, 11, 11, 12, 12, 12, 13, 13, 13, 80
- 平均値:18.7
- 中央値:12.0
平均では「大幅に上昇」したように見えますが、中央値を見ると“実態は変わっていない”ことがわかります。
外れ値である”80”を除外すると
- 平均値:11.9
- 中央値:12.0
となり、平均値が外れ値の影響を大きく受けるのに対し、中央値は影響をほとんど受けていないことが分かります。
例2:工程時間の分布(右に長い分布)
3, 4, 4, 5, 5, 5, 6, 6, 9, 20(分)
- 平均値:7.2
- 中央値:5.0
平均だけを見ると「工程全体が遅い」と判断しますが、中央値を見ると「ほとんどのケースは5分前後」であることがわかり、遅延の原因は“ごく一部の案件”だと判断できます。
まとめ
- 平均は便利だが、外れ値に弱い
- 中央値は安定しやすく、実態を捉えやすい
- 分布が歪んでいる場合は中央値を使用する
- 平均で変動を見る、中央値で実態を見る
- 平均値と中央値を併用し、比べることが重要

の種類-120x68.jpg)

コメント